Visual complex analysis: first chapter exercises

"Visual complex analysis" it's a very good book, with really good exercises.

\(\require{cancel}\)

Complex numbers

Let's start with the main protagonist of this book: complex numbers and the inciting incident that allowed their introduction

$$ i = \sqrt {-1} $$

The following are the main entities associated with complex numbers

$$ \eqalign{ z &= x + i y \cr z &= r e^{i\theta} \cr r &= |z| = \sqrt{x^2 + y^2} \cr \theta &= \arg(z) = \arctan\left(\hbox{Re}(z)\over\hbox{Im}(z)\right)\cr } $$

Transformations and motions

A motion (or isometry) is defined as a mapping that preserves distances; this allows to define two figures to be congruent if it exists a mapping that maps one in the other.

This definition can be refined to include direct and opposite motions: the latter are transformations that need the figure to be "flipped".

Using this we can define a geometry as the invariants of the set of motions.

What are these mappings: there are translations with respect to a complex number \(a\) represented by the operator

$$ T_a(z) = z + a $$

that is simply addition on the complex plane; another basic transformation is represented bythe rotation around the origin by an angle \(\alpha\)

$$ R_0^\alpha(z)=e^{i\alpha}z $$

there are rotations around a point \(a\) of angle \(\theta\) that can be expressed as the composition of a translation from \(a\) to the origin, the rotation of an angle \(\theta\) and then the translation back to \(a\)

$$ R^\theta_a(z) = \left(T_a\circ R_0^\theta\circ T_{-a}\right)(z) = e^{i\theta}\left(z -a\right) + a = e^{i\theta}z + k $$

where \(k = a\left(1 - e^{i\theta}\right)\). This expression makes trivial to write a generic rotation as a rotation around the origin followed by a traslation \(k\)

$$ R^\theta_a = R^\theta_0(z) + k = \left(T_k\circ R^\theta_0\right)(z) $$

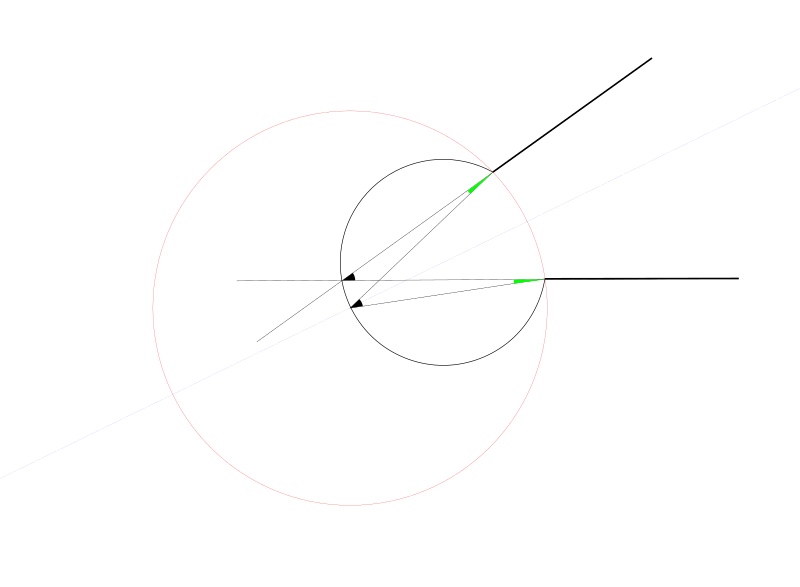
It's always possible to find a transformation that sends two equal length segments into each other: using the diagram below, find the intersection of the lines generated by the segments and use the circle determined by such point end the two extreme of the two segments to move the intersection point along such circumference until an equilateral triangle is formed with the two extremes.

The angle subtended (represented in black) remains the same and the angle formed between the new triangle sides and our segments (represented in green) is half of such angle: this means that now we can rotate around such point to make the segments coincide.

Another kind of transformation is the so called reflections: they intuitively swap points between sides of a line \(L\); they are indicated with

$$ P_L(z) $$

In a certain sense they are the most fondamental transformation because every isometry on the plane can be reduced to two/three reflections.

This is possible because a generic rotation around the point \(a\) with angle \(\theta\) can be performed by two reflections \(P_{L_1}\) and \(P_{L_2}\) where \(L_1\) and \(L_2\) meet at \(a\) with an angle of \(2\theta\).

A generic translation \(T_k\) instead can be expressed by two reflections along two directions parallel to \(k\) at distance \(|k|/2\) from each other.

Exercises

1

The roots of a general cubic equation in \(X\) may be viewed (in the \(XY\)-plane) as the intersection of the \(X\)-axis with the graph of a cubic of the form

$$ Y=X^3+AX^2+BX+C $$

i) Show that the point of inflection of the graph occurs at \(X = -{A\over3}\)

ii) Deduce (geometrically) that the substitution \(X = \left(x - {A\over3}\right)\) will reduce the above equation to the form \(Y=x^3+bx+c\).

iii) Verify this by calculation.

i

Using the derivative with respect to \(x\) we have

$$ \eqalign{ Y^\prime &= 3X^2+2AX+B\cr Y^{\prime\prime} &= 6X+2A\cr } $$

The point of inflection is for the second equation equal to zero, givin the expected result.

ii

Let's do some basic function analysis of this cubic equation: first of all we have

$$ \eqalign{ \lim_{X\to\infty}Y(X) &= \infty\cr \lim_{X\to-\infty}Y(X) &= -\infty\cr } $$

since the function is continuous means that there is at least one point crossing the \(x\) axis and so one root.

From the first derivative of the function we know that the extreme of the function are at the solutions of the equation \(3X^2+2AX+B=0\), a quadratic polynomial

$$ \eqalign{ X_{l,r} &= {-2A\pm\sqrt{4A^2-4\cdot3\cdot B}\over6}\cr &=-{A\over3}\pm{\sqrt{A^2 - 3B}\over3} \cr &=X_I\pm{\sqrt{\delta_{AB}}\over3} \cr &=X_I+\Delta_{l,r} \cr } $$

So the maximum/minimum/inflexion points form a symmetry.

$$ \eqalign{ Y(X_I+\Delta_{l,r}) &= \left(X_I+\Delta_{l,r}\right)^3 + A\left(X_I+\Delta_{l,r}\right)^2 + B\left(X_I+\Delta_{l,r}\right) + C \cr &=\underline{X_I^3}+3X^2_I\Delta_{l,r}+3X_I\Delta_{l,r}^2+\Delta^3_{l,r} \cr &\phantom{=}+\underline{AX^2_I}+2AX_I\Delta_{l,r}+A\Delta_{l,r}^2 \cr &\phantom{=}+\underline{BX_I}+B\Delta_{l,r} \cr &\phantom{=}+\underline{C} \cr &= Y(X_I) + \Delta_{l,r}^3 + \left(3X_I + A\right)\Delta_{l,r}^2 + \left(3X^2_I+2AX_I + B\right)\Delta_{l,r} \cr &= Y(X_I) + Y^\prime(X_I)\Delta_{l,r} + Y^{\prime\prime}(X_I)\Delta_{l,r}^2 + \Delta_{l,r}^3 \cr } $$

Since \(X_I\) it's the inflexion point, the term quadratic in \(\Delta_{l,r}\) is removed, and since \(\Delta_l = -\Delta_r\) we have

$$ \eqalign{ Y(X_l) - Y(X_I) = Y(X_I + \Delta_l) - Y(X_I) &= Y^\prime(X_I)\Delta_l + \Delta_l^3 \cr &= -Y^\prime(X_I)\Delta_r - \Delta^3_r \cr &= -\left(Y(X_I + \Delta_r) - Y(X_I)\right) = -\left(Y(X_r) - Y(X_I)\right)\cr } $$

so the inflexion point is equidistant between these points (both vertically and horizontally).

Notice that the first derivative at \(X_I\) is related to the discriminant

$$ \eqalign{ Y^\prime(X_I) &= 3\left(-{A\over3}\right)^2 + 2 A\left(-{A\over3}\right) + B \cr &= {A^2\over3} - 2{A^2\over3} + B \cr &= -{A^2\over3} + B \cr &= -{1\over3}\left(A^2 - 3B\right) \cr &= -{1\over3}\delta_{AB} \cr } $$

This means that if the first derivative at the inflexion point is positive, then there are not max/min.

There is also a simmetry more general

$$ \eqalign{ Y(-X) - C &= \left(-X\right)^3 + A\left(-X\right)^3 \cr &= -\left(Y(X) - C\right) \cr } $$

where it's good to remember that \(Y(0)=C\) means the point where the curve intersects with the \(y\) axes, so \(y = C\) it's a axes of symmetry of the curve (you could translate it ).

2

In order to solve the cubic equation \(x^3 = 3px+2q\), do the following

i) Make the inspired substitution \(x = s + t\), and deduce that \(x\) solves the cubic if \(st = p\) and \(s^3 + t^3 = 2q\).

ii) Eliminate \(t\) between these two equations, thereby obtaining a quadratic equation in \(s^3\).

iii) Solve the quadratic to obtain the two possible values of \(s^3\). By symmetry, what are the possible values of \(t^3\)?

iv) Given that we know that \(s^3 + t^3 = 2q\) deduce the formula (1.4).

i

$$ \eqalign{ x^3 &= 3px + 2q \cr \left(s + t\right) &= 3p\left(s + t\right) + 2q \cr s^3 + 3s^2t + 3st^2 + t^3 &= 3ps + 3pt + 2q \cr 3\left(st\right)\left(s + t\right) + s^3 + t^3 &= 3p\left(s + t\right) + 2q \cr } $$

ii

From \(st = p\) we can rewrite

$$ \eqalign{ s^3 + t^3 &= 2q \cr s^3 + \left(p\over s\right)^3 &= 2q \cr s^6 - 2qs^3 + p^3 &= 0 \cr } $$

iii

From the previous point we can solve wrt \(s^3\)

$$ s^3_\pm = q\pm\sqrt{q^2 - p^3} $$

Since the starting equation is symmetric wrt \(t\) it has the same solution. Or we can use the sign to differentiate them.

iv

$$ x = s + t = \root 3 \of{q + \sqrt{q^2 - p^3}} + \root 3 \of{q - \sqrt{q^2 - p^3}} $$

4

Here is a basic fact about integers that has many uses in number theory: if two integers can be expressed as the sum of two squares, then so can their product. With the understanding that each symbol denotes an integer, this says that if \(M = a^2 + b^2\) and \(N=c^2 + d^2\), then \(MN = p^2 + q^2\). Prove this result by considering \(|\left(a + \imath b\right)\left(c + \imath d\right)|\)

Solution

$$ \eqalign{ p^2 + q^2 = |p + \imath q|^2 = |\left(a + \imath b\right)\left(c + \imath d\right)|^2 &= |\left(ac - bd\right) +\imath \left(bc + ad\right)|^2 \cr &= \left[ \left(ac - bd\right) +\imath \left(bc + ad\right) \right] \left[\left(ac - bd\right) -\imath \left(bc + ad\right)\right] \cr &=\left(ac - bd\right)^2 + \left(bc + ad\right)^2 \cr &=a^2c^2 - \cancel{2abcd} + b^2d^2 + b^2c^2 + \cancel{2abcd} + a^2d^2 \cr &= a^2 \left(c^2 + d^2\right) + b^2\left(c^2 + d^2\right) \cr &= \left(a^2 + b^2\right) \left(c^2 + d^2\right) \cr } $$

5

The figure below shows how two similar triangles may be used to construct the product of two complex numbers. Explain this.

Solution

Triangles are similar if the length of corresponding sides are proportional; in our case this is true since we have the ratio of corresponding sides equal to \(b\), i.e.

$$ {ab\over a} = {b\over1} \; \hbox{and} \; {ab - b\over a - 1} = {b\over1} $$

6

i) if \(c\) is a fixed complex number, and \(R\) is a fixed real number, explain with a picture why \(|z - c|\) is the equation of a circle.

ii) given that \(z\) satisfies the equation \(|z + 3 -4i| = 2\), find the minimum and maximum values of \(|z|\), and the corresponding positions of \(z\).

solution to point i

It describes a circle because it's the locus of points with distance \(R\) from \(c\), more explicitly, start with a point \(z\) such that \(\hbox{Im}(z)=\hbox{Im}(c)\) and \(\hbox{Re}(z) = \hbox{Re}(c) + R\), this satisifies our equation; from here we can generate the other point from it via

$$ z = c + Re^{i\theta} $$

solution to point ii

For the module of \(z\) we have

$$ \eqalign{ |z| = |c + Re^{i\theta}| &= \sqrt{\hbox{Re}^2(c + Re^{i\theta}) + \hbox{Im}^2(c + Re^{i\theta})} \cr &= \sqrt{\left(\hbox{Re}(c) + \hbox{Re}(Re^{i\theta})\right)^2 + \left(\hbox{Im}(c) + \hbox{Im}(Re^{i\theta})\right)^2} \cr &= \sqrt{\left(\hbox{Re}(c) + R\cos\theta\right)^2 + \left(\hbox{Im}(c) + R\sin\theta\right)^2} \cr &= \sqrt{\hbox{Re}^2(c) + 2R\hbox{Re}(c)\cos\theta + R^2\cos^2\theta + \hbox{Im}^2(c) + 2R\hbox{Im}(c)\sin\theta + R^2\sin^2\theta} \cr &= \sqrt{|c|^2 + R^2 + 2R\left(\hbox{Re}(c)\cos\theta + \hbox{Im}(c)\sin\theta\right)} \cr } $$

Using the usual tecnique it's possible to say that for \(\tan\theta = \hbox{arg}(c)\) we have a minimum; for the case in the exercise \(c=4i - 3\), corresponding to

$$ \theta = \arctan\left(\hbox{Im}(c)\over\hbox{Re}(c)\right) = \arctan\left(-{4\over3}\right) $$

7

Use a picture to show that if \(a, b\in\mathbb{C}\) then

$$ |z - a| = |z - b| $$

it is the equation of a line.

Solution

Both sides of the equation, for a specific \(z\), individuate a circle each; if we take the circle with center in \(a\) passing through \(b\) and viceversa we have two points satisfying the equation. The line passing through these two points is the locus of the points satisfying the equation.

In particular from the picture is clear that \(z,a, b\) form an isoscele triangle given the constraint from the equation.

8

Let \(L\) be a straight line in \(\mathbb{C}\) making an angle \(\phi\) with the real axis, and let \(d\) be its distance from the origin. Show geometrically that if \(z\) is any point on \(L\) then

$$ d = \left\vert\hbox{Im}\left(e^{-i\phi}z\right)\right\vert $$

Solution

If \(z\) is on the line this means that

$$ \left\lbrace\eqalign{ \alpha &= \pi/2 - \phi \cr \beta &= \pi/2 + \phi - \theta \cr \gamma &= \theta - \phi \cr }\right. $$

\(z\) can be expressed in polar form like \(z = |z|e^{i\theta}\) and the distance can be intepreted as the side \(QO\) of the right triangle \(QzO\) given by

$$ \eqalign{ d &= \sin\gamma|z| = \cr &= |z|sin\left(\theta - \phi\right) \cr &= \hbox{Im}\left[|z|e^{i\left(\theta - \phi\right)}\right] \cr &= \hbox{Im}\left[|z|e^{i\theta}e^{-i\phi}\right] \cr &= \hbox{Im}\left[ze^{-i\phi}\right] \cr } $$

9

Let \(A\), \(B\), \(C\), \(D\) be four points on the unit circle. If \(A + B + C + D = 0\), show that the points must form a rectangle.

Solution

Since the points are on the unit circle, the first basic property is

$$ |A| = |B| = |C| = |D| = 1 $$

then rearranging the equation we obtain

$$ \eqalign{ A + B &= -(C + D) \cr B + C &= -(D + A) \cr C + A &= -(B + D) \cr } $$

this means that partitioning the points in pairs, the sums of the pairs must be opposite complex numbers; this can be useful since from the diagram

it's obvious that the sum of two complex numbers on the unit circle is a vector bisecting the two complex numbers themselves, so the module of the vector identifies completely the angle between the two starting complex numbers.

Since opposite pairs have opposite sum vectors, means that they share the same angle between them and the line formed from the sums is a symmetry axis.

So, if \(\alpha\) it's the angle between the bisect and one vector for the first pair and \(\beta\) the angle for the complementar pair, then we have $$ 4\alpha + 4\beta = 2\pi \to \alpha+\beta = {\pi\over2} $$

but \(\alpha+\beta\) it's the angle between complementar bisects.

10

Show geometrically that if \(|z|=1\) then

$$ \hbox{Im}\left[z\over\left(z + 1\right)^2\right] = 0 $$

Apart from the unit circle, what other points satisfy this equation?

Solution

From the diagram it's apparent that the argument of the complex number \(z + 1\) it's half the argument of \(\theta = \arg(z)\) (the triangles formed by \(z\), the origin , \(1\) and \(z + 1\) are similar)

Squaring \(z + 1\) doubles its argument, meanwhile the division substracts its argument from the argument of \(z\) resulting in a complex number with \(\arg\) equal to zero.

The set that satisfies the equation are the points on the real axis: having the argument equal to zero makes all the operations described above collapse on the real axis itself (the bisect of angle of zero is the angle itself).

11

Explain geometrically why the locus of \(z\) such that

$$ \arg\left(z - a\over z - b\right) = \hbox{constant} $$

is an arc of a certain circle passing through the fixed points \(a\) and \(b\).

Solution

The expression \(\arg\left(z - a\over z - b\right)\) is equal to the angle between the complex number \(z - a\) and \(z - b \); it's a well known fact that the inscribed angle is a constant, so that's proven; let's state explicitly this fact and talk about it since will be useful in the following exercises: Inscribed angle theorem: the angle \(\theta\) inscribed in a circle is half of the central angle that subtends the same arc on the circle.

the red part in the above picture is the actual part of the circle that the theorem is talking about, i.e. the part that comprehends the center of the circle, otherwise the angle is greater than \(\pi/2\) (in the picture represented in blue).

That means that there is a discontinuity between the red and blue part.

An interesting aspect is the distance between the center \(O\) of the circle and the segment \(\overline{ab}\): let \(M\) the midpoint between the points \(a\) and \(b\) then we have

$$ d(O,M) = {d(a, b)\over2\tan\left(\theta\right)} = L\left(\theta\right) $$

So we have \(\lim_{\theta\to0}L(\theta) = \infty\) and \(\lim_{\theta\to\pi/2}L(\theta)\to0\).

Re-expressing \(L(\theta)\) in term of \(z\) we have

$$ L(\theta) = {|z|\over2\arg\left(a - 0\over b - 0\right)} $$

12

By using pictures, find the locus of \(z\) for each of the following equations

$$ \hbox{Re}\left(z -1 - i\over z + i + 1\right) = 0\;\hbox{and}\;\hbox{Im}\left(z-1-i\over z +1 +i\right) = 0 $$

Solution

Using the previous exercise we can say that the first equation implies \(\arg(\dots) = \pi/2\)

13

Find the geometric configuration of the points \(a\), \(b\) and \(c\) if

$$ {b-a\over c - a} = {a - c\over b -c} $$

[Hint: Separately equate the lengths and the angles of the two sides]

Solution

Let rewrite the equation using

$$ \left\lbrace\eqalign{ P &= b - a \cr Q &= c - a \cr R &= b - c \cr }\right. $$

with the extra relation \(Q + R - P = 0\). This can be represented with the following picture:

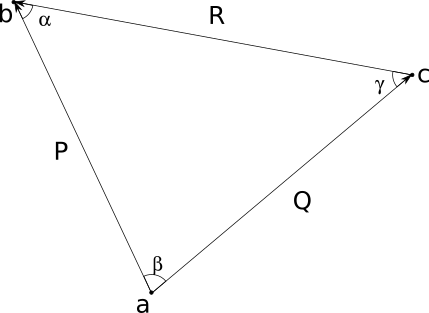
where the initial relation becomes

$$ {P\over Q} = -{Q\over R} $$

Writing in polar notation this can be expressed as

$$ {R_P e^{i\theta_P}\over R_Q e^{i\theta_Q}} = e^{i\pi} {R_Q e^{i\theta_Q}\over R_R e^{i\theta_R}}\longrightarrow {R_P \over R_Q} e^{i\left(\theta_P - \theta_Q\right)} = {R_Q\over R_R} e^{i\left(\pi + \theta_Q - \theta_R\right)} $$

that takes as to two separate equations

$$ \left\lbrace \eqalign{ & {R_P\over R_Q} = {R_Q\over R_R} \cr & \theta_P - \theta_Q = \pi + \theta_Q - \theta_R \cr }\right. $$

It's possible to express the triangle's angles with respect to the arguments of our complex numbers:

$$ \left\lbrace \eqalign{ \beta = \theta_P - \theta_Q \cr \pi - \gamma = \theta_R - \theta_Q \cr } \right. $$

that allows us to assume that \(\beta = \gamma\). Now we can use the law of sines for a generic triangle to say that

$$ {R_P\over\sin\gamma} = {R_Q\over\sin\alpha} = {R_R\over\sin\beta} $$

but this means that

$$ \left\lbrace \eqalign{ {R_P\over R_Q} &= {\sin\gamma\over\sin\alpha} \cr {R_Q\over R_R} &= {\sin\gamma\over\sin\beta} \cr }\right. $$

so also \(\alpha = \beta\) holds; this means that the initial equation identifies equilateral triangles.

14

By considering the product \(\left(2 + i\right)\left(3 + i\right)\), show that

$$ {\pi\over4} = \arctan\left(1\over2\right) + \arctan\left(1\over3\right) $$

Solution

The relation can be obtained comparing the polar version of the product

$$ \left(2 + i\right)\left(3 + i\right) = 5\left(1 + i\right) = 5\sqrt2 e^{i{\pi\over4}} $$

$$ \sqrt{5}e^{i\arctan\left(1\over2\right)}\cdot\sqrt2\sqrt5 e^{i\arctan\left(1\over3\right)} = 5\sqrt2 e^{i\left(\arctan\left(1\over2\right) + \arctan\left(1\over3\right)\right)} $$

15

Draw \(e^{i{\pi\over4}}\), \(e^{i{\pi\over2}}\), and their sum. By expressing each of these numbers in the form \(x +iy\) deduce that

$$ \tan\left(3\pi\over8\right) = 1+\sqrt2 $$

Solution

The sum is

$$ e^{i{\pi\over4}} + e^{i{\pi\over2}} = {1\over\sqrt2} + i\left(1 + {1\over\sqrt2}\right) $$

from this we can calculate the \(\arg\) for it

$$ {1 + {1\over\sqrt2}\over{1\over\sqrt2}} = 1 + \sqrt2 $$

Taking into account that the sum is identifying the bisector between the two angle (i.e. \({3\pi\over8}\)) we have the desired result.

16

Starting from the origin, go one unit east, then the same length north, then \({1\over2}\) of the previous length west, then \({1\over3}\) of the previous length south, then \({1\over4}\) of the previous length east and so on. What point does this "spiral" converge to?

Solution

The first terms of this succession are

$$ z_0 = 0,\,z_1=z_0 + 1,\,z_2=z_1 + i,\,z_3 = z_2 + {1\over2} $$

In general we have the relation

$$ z_{k+1} = z_k + \Delta_{k+1} $$

where \(\Delta_{k+1} = {\left|\Delta_k\right|\over k}i^k\). Unrolling the succession we have

$$ \eqalign{ z_{k+1} &= z_k + \Delta_{k+1} \cr &= z_{k - 1} + \Delta_{k} + \Delta_{k+1} \cr &= \sum_{j=0}^{k+1} \Delta_k \cr &= \sum_{j=0}^{k+1}{i^j\over j!} \cr \lim_{k\to\infty}z_{k+1} &= e^i \cr } $$

17

If \(z=e^{i\theta}\not-1\), then \(z - 1 = i\tan\left(\theta\over2\right)\left(z + 1\right)\). Prove this (i) by calculation, (ii) with a picture

Solution to i

Taking in mind that

$$ \tan\left(\theta\over2\right) = {\sin\theta\over1 + \cos\theta} = {1 - cos\theta\over\sin\theta} $$

so we can rewrite the right hand side as $$ \eqalign{ i\tan\left(\theta\over2\right)\left(z + 1\right) &=i\tan\left(\theta\over2\right)\left(cos\theta + 1 + i\sin\theta\right) \cr &=i\left\lbrack{\sin\theta\over 1 + \cos\theta}\left(\cos\theta + 1\right) + {1 - \cos\theta\over\sin\theta}i\sin\theta\right\rbrack \cr &=i\sin\theta - 1 +\cos\theta\cr &=z - 1 \cr } $$

Solution to ii

18

Prove that

$$ e^{i\theta} + e^{i\phi} = 2\cos\left(\theta - \phi\over2i\right) e^{i{\left(\theta+\phi\right)\over2}} $$

$$ e^{i\theta} - e^{i\phi} = 2i\sin\left(\theta - \phi\over2\right) e^{i{\theta+\phi\over2}} $$

(i) by calculation, and (ii) with a picture.

Solution to i

$$ \eqalign{ e^{i\theta} + e^{i\phi} &= \left(\cos\theta + i \sin\theta\right) + \left(\cos\phi + i\sin\phi\right) \cr &= \cos\theta + \cos\phi + i\left(\sin\theta+\sin\phi\right) \cr &=2\cos\left(\theta + \phi\over2\right)\cos\left(\theta-\phi\over2\right) + i\left\lbrack2\sin\left(\theta+\phi\over2\right)\cos\left(\theta-\phi\over2\right)\right\rbrack \cr &=2\cos\left(\theta-\phi\over2\right)\left\lbrack \cos\left(\theta+\phi\over2\right) + i\sin\left(\theta+\phi\over2\right) \right\rbrack \cr &=2\cos\left(\theta-\phi\over2\right) e^{i{\theta+\phi\over2}} \cr } $$

19

The "centroid" \(G\) of a triangle \(T\) is the intersection of its medians. If the vertices are the complex numbers \(a,b,c\) then you may assume

$$ G={1\over3}\left(a + b + c\right) $$

On the side of \(T\) we have constructed three similar triangles of arbitrary shape, so producing a new triangle with vertices \(p, q, r\). Using complex algebra, show that the centroid of the new triangle is in exactly the same place as the centroid of the old triangle.

Solution

Since we are using similar triangles, we have the new vertices at a fixed angle with respect to the "old" side so

$$ \left\lbrace\eqalign{ p &= a + L\cdot (b - a)\cdot e^{i\theta} \cr q &= b + L\cdot (c - b)\cdot e^{i\theta} \cr r &= c + L\cdot (a - c)\cdot e^{i\theta} \cr }\right. $$

This means that the new centroid

$$ \eqalign{ G^\prime &= {1\over3}\left(p + q + r\right) \cr &= {1\over3}\left(a + b + c\right) + L e^{i\theta}\left(\left(b - a\right) + \left(c - b\right) + \left(a - c\right)\right) \cr &= G \cr } $$

coincides with the old one.

20

Show that it is impossible to draw an equilateral triangle such that all three vertices are Gaussian integers.

Solution

If a triangle is equilateral means that also its angles are all the same, i.e. \({\pi\over3}\), now imagine you have two vertices \(a\) and \(b\) on integers, this means that

$$ \hbox{Re}(b - a)\in\mathbb{N}\;\hbox{and}\;\hbox{Im}(b - a)\in\mathbb{N} $$

Then \(c -a = (b - a) e^{i\pi/3} \), this can be expanded further

$$ \eqalign{ c - a &= (b - a) e ^{i\pi/3} \cr &= \left(\hbox{Re}\left(b - a\right) + i\hbox{Im}\left(b - a\right)\right)\left(\cos\left(\pi\over3\right) + i\sin\left(\pi\over3\right)\right) \cr &= \hbox{Re}\left(b - a\right)\cos\left(\pi\over3\right) + i \hbox{Re}\left(b - a\right)\sin\left(\pi\over3\right) +i \hbox{Im}\left(b - a\right)\cos\left(\pi\over3\right) - \hbox{Im}\left(b - a\right)\sin\left(\pi\over3\right)\cr &= \left(\hbox{Re}\left(b - a\right)\cos\left(\pi\over3\right) - \hbox{Im}\left(b - a\right)\sin\left(\pi\over3\right)\right) +i\left(\hbox{Re}\left(b - a\right)\sin\left(\pi\over3\right) + \hbox{Im}\left(b - a\right)\cos\left(\pi\over3\right)\right) \cr &= \left(\hbox{Re}\left(b - a\right)\left(1\over2\right) - \hbox{Im}\left(b - a\right)\left(\sqrt{3}\over2\right)\right) +i\left(\hbox{Re}\left(b - a\right)\left(\sqrt{3}\over2\right) + \hbox{Im}\left(b - a\right)\left(1\over2\right)\right) \cr } $$

Since \({\sqrt{3}\over2}\not\in\mathbb{N}\) it means that both the component of the complex number \(c\) cannot be an integer either.

23

Draw an arbitrary triangle, and on each side draw an equilateral triangle lying outside the given triangle. What do you suspect it's special about the new triangle formed by joining the centroids (cf ex.19) of the equilateral triangles?

Use complex algebra to prove that you are right. What happens if the equilateral triangles are instead drawn on the inside of the given triangle?

Solution

Using ex.19 we can say for sure that the new centroid is coincides with the old one.

24

From \(\left(1.15\right)\) we know that

$$ 1 + z + z^2 + \cdots + z^{n - 1} = {z^n - 1\over z - 1} $$

i) In what region of \(\mathbb{C}\) must lie in order that the infinite series converges

ii) if \(z\) lies in this region, to which point in the plane the infinite series converges?

iii) In the spirit of figure [1.9], draw a large, accurate picture of the infinite series in the case \(z = {1\over2}\left(1 + i\right)\), and check that it does indeed converges to the point predicted by part (ii).

Solution to part i

Let \(S_n = {z^n - 1\over z - 1}\) be the partial sum, and \(\hat S_n = 1 + |z| + \cdots + |z|^{n + 1} = {|z|^n - 1\over|z| - 1}\) the partial sum for the corresponsing series of absolute values.

We know that

$$ \forall n\in\mathbb{N}\;\hat S_n > |S_n| $$

moreover we know that \(\hat S_n < {|z|^n\over |z| - 1}\) and the right hand side converges for \(|z| < 1\).

Solution to part ii

If we write a complex number inside the unit disk as \(z = R e^{i\theta}\), we can rewrite the partial sum like

$$ \eqalign{ \lim_{n\to\infty}{z^n - 1\over z - 1} &= \lim_{n\to\infty} \cr &= \lim_{n\to\infty}{R^n e^{in\theta} - 1\over R e^{i\theta} - 1} \cr &= \lim_{n\to\infty}{R^n e^{in\theta} - 1\over z - 1} \cr &= {1\over 1 - z} \cr } $$

Solution to part iii

Using the formula just deducted we have

$$ \lim_{n\to\infty}S_n\left({1\over2}\left(1 + i\right)\right) = {1\over 1 - {1\over2}\left(1 + i\right)} = 1 + i $$

25

Let

$$ S = \cos\theta + \cos3\theta + \cos5\theta + \cdots + \cos\left(2n - 1\right)\theta $$

show that

$$ S = {\sin\left(2n\theta\right)\over2\sin\theta}\hbox{ or equivalently } S={\sin\left(n\theta\right)\cos\left(n\theta\right)\over\sin\theta} $$

Solution

Let's start with

$$ \cos\left(k\theta\right) = {e^{ik\theta} + e^{-ik\theta}\over2} $$

this means that

$$ \eqalign{ 2S &= 2\sum_{k = 1}^n \cos\left(2k - 1\right)\theta \cr &= \sum_{k = 1}^n\left(e^{ik\theta} + e^{-ik\theta}\right) \cr &= \sum_{k = 1}^n e^{i\left(2k - 1\right)\theta} + \sum_{k = 1}^n e^{-i\left(2k - 1\right)\theta} \cr &= \sum_{k = 1}^n \left(e^{i\theta}\right)^{2k - 1} + \sum_{k = 1}^n \left(e^{-i\theta}\right)^{2k - 1} \cr &= \sum_{k = 0}^{n - 1} \left(e^{i\theta}\right)^{2k + 1} + \sum_{k = 0}^{n - 1} \left(e^{-i\theta}\right)^{2k + 1} \cr &= e^{i\theta}\sum_{k = 0}^{n - 1}\left(e^{i2\theta}\right)^k + e^{-i\theta}\sum_{k = 0}^{n - 1}\left(e^{-i2\theta}\right)^k \cr &= e^{i\theta}\left(e^{i2n\theta} - 1\over e^{i2\theta} - 1\right) + e^{-i\theta}\left(e^{-i2n\theta}- 1\over e^{-i2\theta} - 1\right) \cr &= e^{i\theta}{e^{i2n\theta} - 1\over e^{i\theta}\left(e^{i\theta} - e^{-i\theta}\right)} + e^{-i\theta}{e^{-i2n\theta}- 1\over e^{-i\theta}\left(e^{-i\theta} - e^{i\theta}\right)} \cr &= {e^{i2n\theta} - 1\over e^{i\theta} - e^{-i\theta}} + {e^{-i2n\theta} - 1\over e^{-i\theta} - e^{i\theta}} \cr &= {e^{i2n\theta} - 1\over e^{i\theta} - e^{-i\theta}} - {e^{-i2n\theta} - 1\over e^{i\theta} - e^{-i\theta}} \cr &= {\sin\left(2n\theta\right)\over\sin\theta} } $$

For the other side of the equivalence we need just to split the square

$$ \eqalign{ 2\sin\left(2n\theta\right) &= e^{i2n\theta} - e^{-i2n\theta} \cr &= \left(e^{in\theta} - e^{-in\theta}\right)\left(e^{in\theta} + e^{-in\theta}\right) \cr &= 2\sin\left(n\theta\right)\cdot 2\cos\left(n\theta\right) \cr } $$

26

i) By considering \(\left(a + ib\right)\left(\cos\theta + i\sin\theta\right)\) show that

$$ b\cos\theta + a\sin\theta = \sqrt{a^2+b^2}\sin\left(\theta + \arctan\left(b\over a\right)\right) $$

ii) use the previous result to prove by the method of induction

$$ {d\over dt^n}\left(e^{at}\sin bt\right) = \left(a^2 + b^2\right)^{n/2}\sin\left(bt + n \arctan\left(b\over a\right)\right) $$

Solution to part i

It's enough to explicitly calculate the real and imaginary part

$$ \eqalign{ \left(a + ib\right)\left(\cos\theta + i\sin\theta\right) &= a\cos\theta - b\sin\theta + i\left(b\cos\theta+a\sin\theta\right) \cr &= z e^{i\theta} \cr &= |z| e^{i\left(\theta + \arg(z)\right)} \cr &= \sqrt{a^2 + b^2}\left[\cos\left(\theta + \arg(z)\right) + i\sin\left(\theta + \arg(z)\right)\right] \cr } $$

Solution to part ii

Using the fact that \({d\over dt}\left(e^{a t}e^{ibt}\right) = (a + ib)\left(e^{a t}e^{ibt}\right)\) and assuming that the general form of the equation is

$$ {d\over dt^n} \left(e^{at} e^{ibt}\right) = R(n, a, b)\left( \cos\phi(n,a,b) + i\sin\phi(n,a,b)\right) $$

since the imaginary part operator it's linear we know that

$$ \left\lbrace \eqalign{ R(n, a, b) &= e^{at} \left(a^2 + b^2\right)^{n/2} \cr \phi(n, a, b) &= bt + \arctan\left(b\over a\right) \cr }\right. $$

so now we can write

$$ \eqalign{ {d\over dt^{n + 1}}\left[e^{at} e^{ibt}\right] &= (a + ib){d\over dt^{n}}\left[e^{at} e^{ibt}\right] \cr &= (a + ib)R(n, a, b)\left( \cos\phi(n,a,b) + i\sin\phi(n,a,b)\right) \cr } $$

but then

$$ \eqalign{ R(n + 1, a, b)\sin\phi(n + 1, a, b) &= R(n, a, b)\left(b\cos\phi(n, a, b) + a\sin\phi(n, a, b)\right) \cr &= \left(a^2 + b^2\right)^{n/2}\sqrt{a^2 + b^2}\sin\left[\phi(n, a, b) + \arctan\left(b\over a\right)\right] \cr &= \left(a^2 + b^2\right)^{(n + 1)/2}\sin\left[bt + (n + 1) \arctan\left(b\over a\right)\right] \cr } $$

27

Show that the polar form equation of the spiral \(Z(t) = e^{at} e^{ibt}\) in [1.15b] is \(r = e^{(a/b)\theta}\)

Solution

The spiral has two different part, \(e^{at}\) that impacts only the module and \(e^{ibt}\) that impacts only the argument. We can rewrite

$$ \left\lbrace\eqalign{ |z(t)| &= r = e^{at} \cr \arg(z(t)) &= \theta = bt \cr }\right. $$

if we use the relation \(t = {\theta\over b}\) then

$$ r = e^{at} = e^{{a\over b}\theta} $$

28

Reconsider the spiral \(Z(t) = e^{at} e^{ibt}\) in [1.15b], where \(a\), \(b\) are fixed real numbers. Let \(\tau\) be a variable real number. According to (1.9)

$$ z\Leftarrow F_\tau(z) = \left(e^{a\tau} e^{ib\tau}\right)z $$

is an expansion of the plan by factor \(e^{a\tau}\) combined with a rotation of the plan through an angle \(b\tau\).

i) show that \(F_\tau(Z(t)) = Z(t + \tau)\), and deduce that the spiral is an invariant curve of the transformation \(F_\tau\).

ii) use this to give a calculus-free demonstration that all rays from the origin cut the spiral at the same angle.

iii) Show that if the spiral is rotated about the origin through an arbitrary angle, the new spiral is again an invariant curve of each \(F_\tau\).

iv) Argue that the spirals in the previous part are the only invariant curves of \(F_\tau\).

Solution to part i

By simple algebra we can see that

$$ \eqalign{ F_\tau(Z(t)) &= \left(e^{a\tau} e^{ib\tau}\right)e^{at} e^{ibt} \cr &= e^{a(t + \tau)} e^{ib(t + \tau)} \cr &= Z(t + \tau) \cr } $$

and indeed the transformation \(F_\tau\) maps the spiral in itself.

Solution to part ii

Following the diagram below

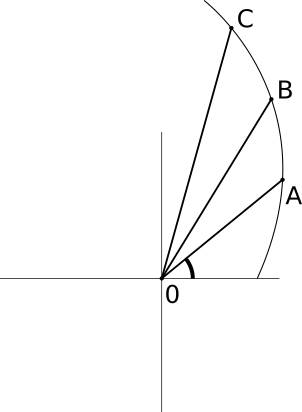
draw rays starting from the origin at fixed angles, multiple of \(\tau\). These rays will determine a family of similar triangles with the same angle \(\tau\) at the origin. The ratio between the sides of the triangles are given by \(e^a\tau\).

This means that the remaining angles are the same, in particular this doesn't depend on the specific value of \(\tau\), so shouldn't change if we take the limit of it to zero.

If we want to explicitly calculate the value the angle \(\alpha\) takes we can use the law of sines

$$ {\sin\left(b\Delta t\right)\over |z(t + \Delta t) - z(t) |} = {\sin\left(\alpha\right)\over|z(t + \Delta t)|} $$

$$ \eqalign{ |z(t + \Delta t)|^2 &= | e^{a(t+\Delta t)} e^{ib(t + \Delta t)}|^2 \cr &= | e^{a\Delta t}e^{ib\Delta t} e^{at} e^{ibt}|^2 \cr &= | e^{a\Delta t}e^{ib\Delta t} z|^2 \cr &= e^{2a\Delta t} |z|^2 \cr |z(t + \Delta t) - z(t)|^2 &= | z(t + \Delta t)|^2 + | z(t)|^2 - \bar z(t + \Delta t)z(t) - z(t + \Delta t)\bar z(t)\cr &= e^{2a(t + \Delta t)} + e^{2at} - e^{a(t + \Delta t)}e^{-ib(t + \Delta t)} e^{at} e^{ibt} - e^{a(t+\Delta t)} e^{ib(t + \Delta t)} e^{at} e^{ibt} \cr &= e^{2a(t + \Delta t)} + e^{2at} - e^{a(2t + \Delta t)}e^{-ib\Delta t} - e^{a(2t+\Delta t)} e^{ib\Delta t} \cr &= e^{2at}\left( e^{2a\Delta t} + 1 - e^{a\Delta t}e^{-ib\Delta t} - e^{a\Delta t} e^{ib\Delta t}\right) \cr &= e^{2at}\left[ e^{2a\Delta t} + 1 - 2e^{a\Delta t}\cos\left(b\Delta t\right)\right] \cr &= e^{2at}e^{a\Delta t}\left[ e^{a\Delta t} + e^{-a\Delta t} - 2\cos\left(b\Delta t\right)\right] \cr &= e^{2at}e^{a\Delta t}\left[ 2\cosh\left(a\Delta t\right) - 2\cos\left(b\Delta t\right)\right] \cr &= 2e^{2at}e^{a\Delta t}\left[ \cosh\left(a\Delta t\right) - \cosh\left(ib\Delta t\right)\right] \cr &= 4e^{2at}e^{a\Delta t}\sinh\left({a + ib\over2}\Delta t\right)\sinh\left({a - ib\over2}\Delta t\right) \cr &= 4e^{a\Delta t}\sinh\left({a + ib\over2}\Delta t\right)\sinh\left({a - ib\over2}\Delta t\right) |z|^2\cr } $$

So we have

$$ \eqalign{ \sin\left(\alpha\right) &= { |z(t + \Delta t)| \over | z(t + \Delta t) - z(t) |} \sin\left(b\Delta t\right)\cr \lim_{\Delta t\to\infty}\sin\left(\alpha\right) &= \lim_{\Delta t\to\infty}{ |z(t + \Delta t)| \over | z(t + \Delta t) - z(t) |} \sin\left(b\Delta t\right)\cr \lim_{\Delta t\to\infty}\sin\left(\alpha\right) &= \lim_{\Delta t\to\infty} {e^{a\Delta t} \sin\left(b\Delta t\right)|z| \over \sqrt{4e^{a\Delta t}\sinh\left({a + ib\over2}\Delta t\right)\sinh\left({a - ib\over2}\Delta t\right)} |z|} \cr &~ \lim_{\Delta t\to\infty} {e^{a\Delta t} b\Delta t\over \sqrt{4e^{a\Delta t}\left({a + ib\over2}\Delta t\right)\left({a - ib\over2}\Delta t\right)}} \cr &= {b\over \sqrt{a^2 + b^2}} \cr } $$

Solution to part iii

To rotate the spiral to an angle \(\theta\)

$$ \eqalign{ Z^\prime(t) &= e^{i\theta}Z(t) \cr &= e^{i\theta}e^{at} e^{ibt} \cr &= e^{at} e^{i(bt + \theta)} \cr } $$

$$ \eqalign{ F_\tau\left[Z^\prime(t)\right] &= \left(e^{a\tau} e^{ib\tau}\right)Z^\prime(t) \cr &= \left(e^{a\tau} e^{ib\tau}\right)\left(e^{at} e^{i(bt + \theta)}\right) \cr &= e^{a(\tau + t)} e^{i\left[b(\tau + t) + \theta\right]} \cr &= Z^\prime(\tau + t) \cr } $$

Solution to part iv

For \(f\) to be an invariant curve means that must exist a reparametrization \(\Lambda\) of the curve such that

$$ F_\tau(f)(t) = f(\Lambda(t)) $$

that can be expressed by the relation

$$ e^{a\tau} e^{ib\tau} f = f\circ\Lambda $$

Extra exercise

Pg 27

Let \(P_n(z) = z^n + Az^{n - 1}+ \dots + Dz + E\) a polynomial with real coefficients, prove that \(P_n(c)=0\) implies \(P_n(\bar c) = 0\) and the factorization contains

$$ \left(z -c\right)\left(z - \bar c\right) = z^2 - \left(c + \bar c\right) + c\bar c = z^2 - 2\Re(c)z + |c|^2 $$