Il formato JPEG
La teoria dell'informazione è in buona parte una formalizzazione della capacità di trasmettere informazione ed un sinonimo della capacità di compressione di un certo stream di simboli; proprio per questo le sue tecniche sono diventate molto importanti nelle tecnologie informatiche ed in alcuni degli ambiti propri dell'informatica hanno permesso la diffusione di "cultura" prima impensabili.
Proprio in merito ad un formato di compressione voglio parlare in questo post,
il formato conosciuto come JPEG. La particolarità di questo formato è che
unisce molte delle caratteristiche dei formati di compressione più comuni, in
particolare la codifica di huffman, la trasformata discreta del coseno
ed una variante del run length encoding. Tutto questo per permettere di
avere una immagine che perde sì qualità rispetto all'immagine originale, ma non
in modo tale da perdere contenuto di informazione ottica.
Ma prima di entrare nei dettagli della specifica un minimo di storia, perché
anche l'informatica è fatta da persone: per prima cosa il nome JPEG
proviene dal J oint P hotographic E xperts G roup, un comitato
che si proponeva il compito di creare uno standard per la diffusione di
immagini tramite internet (questo all'inizio degli anni '90). La sua origine
accademica tuttavia è riconducibile al 1970 all'incirca, quando due ricercatori
cercavano una immagine da inserire all'interno di un loro paper ed essendo
stanchi delle solite immagini decisero di scannerizzare una porzione della pin
up nel paginone centrale di playboy, l'immagine che diventerà poi famosa con il
nome di Lenna
 The first lady of internet
The first lady of internet
Tornando alla implementazione, la specifica del comitato ISO è definita qui ed è riassumibile nei seguenti steps
- Trasformare l'immagine dallo spazio
RGBaYCbCr - downsampling
- Suddividere le immagini in blocchi 8x8 effettuando il padding dove serve
- trasformata discreta del coseno su ognuno dei blocchi
- quantizzazione
- entropy coding e zero length encoding
Analizziamo uno step alla volta.
RGB -> YCbCr
Bene o male chiunque abbia avuto a che fare con la grafica conosce lo spazio
dei colori definito come RGB che sta per red, green e blu, ma
non è il solo sistema possibile
per identificare un colore.
L'identificazione nasce dalla natura fisiologica della visione: l'occhio umano ha una visione tricromatica (caso raro tra i vertebrati che passano da essere tetracromatici a dicromatici)
Ma già dalle lezioni di educazione artistica delle medie sappiamo che esistono almeno due tipologie di schemi di colori, lo schema additivo e lo schema sottrattivo: il primo si basa sulla proprietà additiva della luce in cui si hanno tre colori primari che mescolati generano tramite "addizione" tutti i colori possibili, mentre il secondo è usato nella tipografia (schema CMYK) ed è detto sottrattivo in quanto i colori primari sottraggono ciascuno un colore primario dalla luce riflessa (Il ciano sottrae il rosso, il magenta sottrae il verde ed infine il giallo sottrae il blu). A meno che non vi interessi stampare, lo schema di colori è quello additivo.
Tra gli schemi di colori interessanti nella grafica digitale è il YUV che permette di separare la componente di luminanza (quanto è bianca o nera l'immagine) dalle componenti cromatiche; la scelta di questo schema di colori è importante in quato l'occhio umano è molto più sensibile alla luminanza che alle componenti cromatiche oltre che affermatosi storicamente tramite le trasmissioni televisive in bianco e nero.
Downsampling
Siccome l'occhio umano è più sensibile alla luminanza rispetto alla componente
cromatica, è possibile risparmiare bandwidth diminuendo opportunamente la
quantità di informazione cromatica rispetto all'unità di informazione Y;
questa procedura è standard nel campo delle comunicazioni se teniamo conto che
la trasmissione analogica della programmazione televisiva avviene trasmettendo
la crominanza (UV) con una banda dimezzata rispetto alla luminanza.
Nel caso specifico del JPEG il downsampling può essere effettuato sia
verticalmente che orizzontalmente per ogni componente; nelle specifiche viene
indicato che per ricostruire il rapporto di una dimensione dei blocchi dopo il
downsampling si deve dividere il fattore di sampling di quella componente
rispetto al fattore di sampling più elevato fra le varie componenti, cioé in
pratica se si ha un fattore di sampling per le tre componenti nei rapporti
2:1:1 significa che la prima componente è quella senza subsampling e che le
rimanenti hanno un un numero di pixel dimezzati rispetto a questa.
Di solito il fattore di sampling standard per una immagine JPEG è 2x2, 1x1, 1x1.
MCU
A questo punto, nel caso in cui ci si ritrova con più di una componente si effettua una suddivisione dell'immagine in blocchi 8x8 e un raggruppamento di questi blocchi in delle cosiddette minimal coded unit (MCU, per le immagini ad una sola componente la MCU è il singolo blocco). L'ordinamento delle sequenze dei blocchi è dato dal subsampling: all'interno della MCU i blocchi sono ordinati top-bottom, left-right ed il medesimo ordinamento è seguito dalle MCU all'interno dell'immagine. Per capirci, lo schema usato è il seguente
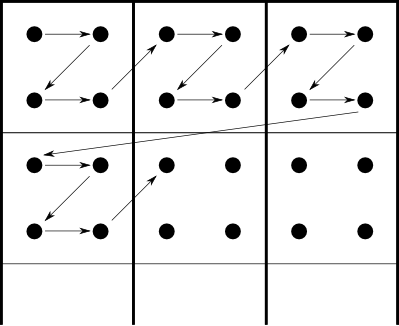
Nella figura i pallini rappresentano i valori della componente, i quadrati interni rappresentano la MCU e le freccie l'ordinamento seguito per l'encoding/decoding
In caso l'immagine non sia di dimensioni tali da avere un numero intero di MCU si completano quelli mancanti aggiungendo valori nulli.
DCT
Si arriva adesso alla parte fondamentale: si effettua la trasformata discreta del coseno che trasforma i 64 valori nel singolo blocco in altri 64 valori che rappresentano i valori delle frequenze corrispondenti del blocco originale; i valori nel punto corrispondente all'angolo alto a sinistra corrisponde alla frequenza più bassa (cioé la frequenza nulla). Le formule per questo passaggio sono $$ S_{u,v} = {1\over 4} C_u C_v \sum_{x=0}^7 \sum_{y=0}^7 S_{xy}\cos{(2x + 1)u\pi\over16}\cos{(2y + 1)v\pi\over16} $$
Quantization
Per diminuire la quantità di informazione necessaria per immagazzinare i valori delle componenti, si definisce una matrice di quantizzazione la quale permette di definire il valore finale dell'entrata del blocco tramite $$ Sq_{ij} = \hbox{round} \left(S_{ij}\over Q_{ij}\right) $$ Questo passaggio è quello che in pratica determina la qualità dell'immagine (se la matrice è composta da elementi tutti uguali all'unità allora la qualità è 100 e l'immagine non perde rispetto all'originale).
Encoding
Il passaggio di encoding vero e proprio avviene a questo punto: per ogni blocco
si effettua un ordinamento delle varie componenti detto a zig zag, in modo da
avere i valori derivanti dalle alte frequenze e quindi meno importanti per la
ricostruzione del valore originale in fondo alla sequenza. Quindi si
differenzia la componente a frequenza \(u, v=0\), detta DC, dalle
rimanenti, dette AC.

La componente DC viene encodata come coppia di valori \((cc, m)\) dove
\(cc\) sta ad indicare il numero di bits che bisogna usare per encodare il
valore di DC in \(m\) usando una rappresentazione in complemento a 2.
Però prima di fare questo il suo valore viene posto uguale alla differenza fra
esso ed il coefficiente precedente (se è il primo blocco allora si prende il
valore reale), questo procedimento è detto differential DC encoding.
Ogni componente AC invece viene encodata come tripletta \((cc,zl,m)\)
dove il primo valore indica quanti bits sono necessari per encodare in una
rappresentazione in complemento a 2 il valore di AC dentro \(m\), mentre
\(zl\) indica quanti valori nulli di AC precedono questo. Esiste una
sequenza particolare che indica l'end of block (EOB) che informa del
fatto che le rimanenti componenti sono nulle e che il blocco è quindi finito;
questo corrisponde a \(cc=0\) e \(zl=0\).
C'è da notare che per i valori di DC si usano 8 bits per rappresentare
\(cc\), mentre ne servono 4 per l'omonimo in AC e altri 4 per \(zl\);
quindi si ha che \(cc\) per DC e la coppia \((cc,zl)\) per AC
vengono memorizzati tramite la codifica di Huffman utilizzando una tabella
separata.
Implementazione
Ovviamente non ritengo di avere espresso esaurientemente l'argomento in quanto
nelle specifiche si parla di quattro tipologie di JPEG di cui non ho
accennato, ma per un approccio iniziale penso che la spiegazione può ritenersi
sufficiente, del resto esiste la specifica che può essere studiata anche da
soli.
Prima di fare un esempio voglio solo indicare come effettivamente è organizzato
un file di immagini in questo formato; prima di tutto le sezioni sono
delimitate inizialmente da un marker composto da due byte, il primo è
sempre 0xff mentre il secondo identifica opportunamente il marker. Grosso
modo quelli più importanti sono i seguenti
| Marker | Output | Significato |
|---|---|---|
| 0xffd8 | Start of file | primo byte del file |
| 0xffc0 | Start of frame | identifica un blocco dell'immagine da decodare a cui seguiranno tabella di Huffman, di Quantizazione etc... qui sono contenute le informazioni riguardanti la dimensione, il numero di colori (1 oppure 3). |
| 0xffc4 | huffman table | ce ne sono 2 o 4 a seconda del numero di colori siccome se ne usa una per la componente AC ed una per la componente DC per luminanza e crominanza separatamente. |
| 0xffdb | Quantization table | unica per tutte le componenti |
| 0xffda | Scan data | contiene zig-zag entropy coded data |
| 0xffd9 | End of JPEG | ultimo byte del file |
ESEMPIO
Dopo i dettagli implementativi, ecco un piccolo esempio con un semplice file di dimensioni 8x8 di colore rosso:
$ hexdump -C <( convert -size 8x8 -quality 100 xc:red jpg:- )
00000000 ff d8 ff e0 00 10 4a 46 49 46 00 01 01 01 00 48 |......JFIF.....H|
00000010 00 48 00 00 ff db 00 43 00 01 01 01 01 01 01 01 |.H.....C........|
00000020 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 |................|
*
00000050 01 01 01 01 01 01 01 01 01 ff db 00 43 01 01 01 |............C...|
00000060 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 |................|
*
00000090 01 01 01 01 01 01 01 01 01 01 01 01 01 01 ff c0 |................|
000000a0 00 11 08 00 08 00 08 03 01 11 00 02 11 01 03 11 |................|
000000b0 01 ff c4 00 14 00 01 00 00 00 00 00 00 00 00 00 |................|
000000c0 00 00 00 00 00 00 09 ff c4 00 14 10 01 00 00 00 |................|
000000d0 00 00 00 00 00 00 00 00 00 00 00 00 00 ff c4 00 |................|
000000e0 15 01 01 01 00 00 00 00 00 00 00 00 00 00 00 00 |................|
000000f0 00 00 09 0a ff c4 00 14 11 01 00 00 00 00 00 00 |................|
00000100 00 00 00 00 00 00 00 00 00 00 ff da 00 0c 03 01 |................|
00000110 00 02 11 03 11 00 3f 00 17 c5 3a fe 1f ff d9 |......?...:....|
0000011f
Linkografia
- Differenza fra RGB e CYMK
- RGB-vs-CMYK
- Specifiche JPEG
- The Scientist and Engineer's Guide to Digital Signal Processing
- Data compression explained
- Bandwidth Versus Video Resolution
- Mia implementazione in C di un parser JPEG
- Digital media primer for geek
- FOURCC.org - your source for video codec and pixel format information.
Comments
Comments powered by Disqus