Modern cryptography: exercises chapter 2 'Perfectly secret encryption'

2018-02-06

Gianluca Pacchiella

Tags:

This post is a work in progress, so if you find it incomplete and not readable probably it's not finished yet. I prefer to publish a little before than leave a post to rust in my drafts.

These are some solved exercises of chapter 2 of the book "Introduction to modern cryptography" by Jonathan Katz and Yehuda Lindell.

I'm not sure are correct but if anyone find any error let me know. It's a work in progress and more exercises will follow in future, when I finally find time to solve more. Also, enjoy my hand made diagrams :).

Notes

An encryption scheme $(\hbox{Gen}, \hbox{Enc}, \hbox{Dec})$ with message space $M$ is perfectly secret if for every probability distribution over $M$, every message $m\in M$, and every ciphertext $c\in C$ for which $\hbox{Pr}\left[C = c\right] > 0$:

$$ \hbox{Pr}\left[M = m\,|\, C = c\right] = \hbox{Pr}\left[M = m\right] $$

This is equivalent to a prior indistinguishibility:

$$ \hbox{Pr}\left[\hbox{Enc}_K(m) = c\right] = \hbox{Pr}\left[\hbox{Enc}_K(m^\prime) = c\right] $$

i.e. the ciphertext's probability distribution is independent from the message's probability distribution.

An important theorem by Shannon tells us that given the encryption scheme $\left(\hbox{Gen}, \hbox{Enc}, \hbox{Dec}\right)$ with message space $M$, for which $|M| = |K| = | C|$. The scheme is perfectly secret if and only if

Every key $k\in K$ is chosen with (equal) probability ${1\over |K|}$ by algorithm $\hbox{Gen}$.
For every $m\in M$ and every $c\in C$, there exists a unique key $k\in K$ such that $\hbox{Enc}_k(m)$ outputs $c$.

A less stricter theorem says instead that if we have a perfectly secret encryption scheme $\left(\hbox{Gen}, \hbox{Enc}, \hbox{Dec}\right)$ with message space $M$, and key space $K$ then $|K| \geq|M|$.

For notation purpose take in mind this way of writing:

$$ \hbox{Pr}\left[C = c\,|\,M = m\right] = \hbox{Pr}\left[\hbox{Enc}_K(M) = c\,|\, M = m\right] = \hbox{Pr}\left[\hbox{Enc}_K(m) = c\right] $$

Instead the adversarial indistinguishability experiment $\hbox{PrivK}^{\hbox{eav}}_{A, \Pi}$ is defined as follow:

The adversary $A$ outputs a pair of messages $m_0, m_1\in M$.
A key $k$ is generated using $\hbox{Gen}$, and a uniform bit $b\in{0,1}$ is chosen. Ciphertext $c\leftarrow\hbox{Enc}_k(m_b)$ is computed and given to $A$. We refer to $c$ as the challenge ciphertext.
$A$ outputs a bit $b^\prime$.
The output of the experiment is defined to be $1$ if $b = b^\prime$, and $0$ otherwise. We write $\hbox{PrivK}^{\hbox{eav}}_{A, \Pi} = 1 $ if the output of the experiment is $1$ and in this case we say that $A$ succeeds.

Exercises

2.1: Prove that, by redefining the key space, we may assume that the key generation algorithm $Gen$ choose a key uniformly at random from the key space, without changing $\hbox{Pr}\left[C = c | M = m\right]$ for any $m, c$.

solution

The encryption scheme can be described using the following diagram:

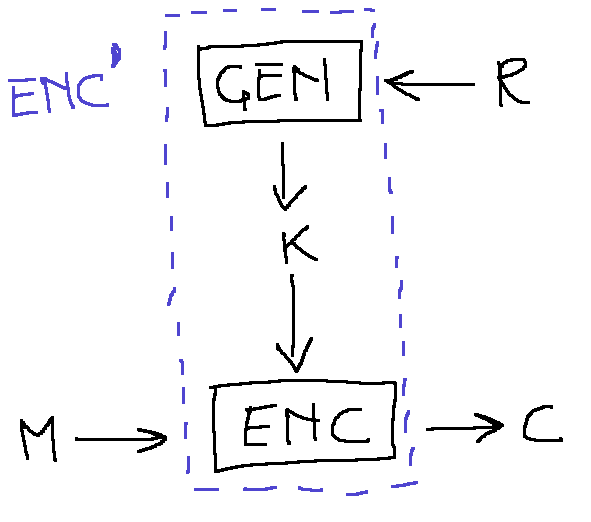
where the $\hbox{Gen}$ algorithm creates a key using a random tape $r$ from the space $R$. Redefining $\hbox{Enc}$ to include $\hbox{Gen}$ and using $r$ as new key we have that

$$ \eqalign{ \hbox{Pr}\left[K=k\right] &= \hbox{Pr}\left[\hbox{Gen}(R)=k\right] \cr &= \sum_r\hbox{Pr}\left[\hbox{Gen}(R)=k\,|\,R = r\right]\hbox{Pr}\left[R = r\right] } $$

This means that we simply shift the key to be the random tape that provides random values to the Turing machine implementing the probabilistic algorithm $\hbox{Gen}$.

we can verify

$$ \eqalign{ \hbox{Pr}\left[ C = c \,|\, M = m\right] &= \hbox{Pr}\left[\hbox{Enc}_K(m) = c\right] \cr &= \sum_k\hbox{Pr}\left[\hbox{Enc}_K(m) \,|\, K = k \right]\cdot\hbox{Pr}\left[K = k\right] \cr &= \sum_k\hbox{Pr}\left[\hbox{Enc}_K(m) \,|\, K = k \right]\cdot\sum_r\hbox{Pr}\left[\hbox{Gen}(R) = k\,|\,R = r\right]\cdot\hbox{Pr}\left[R = r\right] \cr &= \sum_{k, r}\hbox{Pr}\left[\hbox{Enc}_K(m) \,|\, K = k \right]\cdot\hbox{Pr}\left[\hbox{Gen}(R) = k\,|\,R = r\right]\cdot\hbox{Pr}\left[R = r\right] \cr &= \sum_{k, r}\hbox{Pr}\left[\hbox{Enc}_K(m) \,|\, K = k \right]\cdot\hbox{Pr}\left[K = k\,|\,R = r\right]\cdot\hbox{Pr}\left[R = r\right] \cr &= \sum_r\hbox{Pr}\left[\hbox{Enc}^\prime_R(m) \,|\, R = r \right]\cdot\hbox{Pr}\left[R = r\right] \cr &= \hbox{Pr}\left[\hbox{Enc}^\prime_R(m) = m \right] \cr &= \hbox{Pr}^\prime\left[ C = c \,|\, M = m\right] \cr } $$

2.2: Prove that, by redefining the key space, we may assume that $Enc$ is deterministic without changing $\hbox{Pr}\left[C = c \,|\, M = m\right]$ for any $m, c$.

solution

$\hbox{Enc}$ can become deterministic using the random tape as a component of the key;

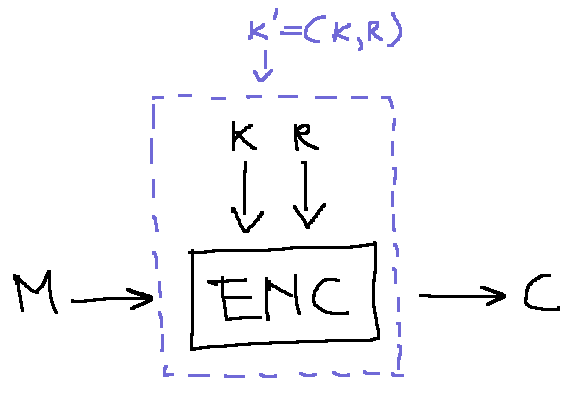
$$ \eqalign{ \hbox{Pr}^\prime\left[C = c\,|\, M = m \right] &= \hbox{Pr}\left[\hbox{Enc}^\prime_k(m = c)\right] \cr &= \sum_{k^\prime}\hbox{Pr}\left[\hbox{Enc}_{k^\prime}(m) = c \,|\, K^\prime = k^\prime\right]\cdot\hbox{Pr}\left[K^\prime = k^\prime\right] \cr &= \sum_{k,\,r}\hbox{Pr}\left[\hbox{Enc}_{k,\,r}(m) = c \,|\, K = k,\,R = r\right]\cdot\hbox{Pr}\left[K = k\right]\cdot\hbox{Pr}\left[R = r\right] \cr &= \sum_k\left(\sum_r\hbox{Pr}\left[\hbox{Enc}_{k,\,r}(m) = c \,|\, K = k,\,R = r\right]\cdot\hbox{Pr}\left[R = r\right]\right)\cdot\hbox{Pr}\left[K = k\right] \cr &= \sum_k\hbox{Pr}\left[\hbox{Enc}_{k}(m) = c \,|\, K = k\right]\cdot\hbox{Pr}\left[K = k\right] \tag{verificare}\cr &= \hbox{Pr}\left[\hbox{Enc}_{k}(m) = c\right] \cr &= \hbox{Pr}\left[C = c\,|\, M = m \right] \cr } $$

Expanding the relation $k^\prime=(k, r)$ we obtain

$$ \eqalign{ \hbox{Pr}\left[K^\prime = k^\prime\right] &= \hbox{Pr}\left[K=k,\, R = r\right] \cr &= \hbox{Pr}\left[K = k\right]\cdot\hbox{Pr}\left[R = r\right] \cr } $$

2.3: Prove or refute: an encryption scheme with message space $M$ is perfectly secret if and only if ($\iff$) for every probability distribution over $M$ and every $c_0,\,c_1\in C$ we have $\hbox{Pr}\left[C = c_0\right] = \hbox{Pr}\left[C = c_1\right]$.

solution

For this one I have not yet a solution but I think has to do with the dimension of the cipher and message space: the iff holds if we take the conditions from the Shannon's theorem, i.e. if the all the spaces have the same dimensions.

2.4: Prove the second direction of Lemma 2.4

solution

We must proof that perfect secrecy implies perfect indistinguishibility; this can be done using the Bayes' theorem

$$ \hbox{Pr}\left[M = m \,|\, C = c\right] = {\hbox{Pr}\left[C = c \,|\, M = m\right]\cdot\hbox{Pr}\left[M = m\right]\over\hbox{Pr}\left[C = c\right]} $$

together with perfect secrecy

$$ \hbox{Pr}\left[M = m \,|\, C = c\right] = \hbox{Pr}\left[M = m\right] $$

to obtain

$$ \eqalign{ {\hbox{Pr}\left[C = c \,|\, M = m\right]\cdot\hbox{Pr}\left[M = m\right]\over\hbox{Pr}\left[C = c\right]} &= \hbox{Pr}\left[M = m\right] \cr {\hbox{Pr}\left[C = c \,|\, M = m\right]\over\hbox{Pr}\left[C = c\right]} &= 1 \cr } $$

2.5: Prove Lemma 2.6.

solution

We need to proof that

$$ \hbox{Pr}\left[\hbox{PrivK}_{A,\Pi}^{\hbox{eav}} = 1\right] = {1\over 2}\iff \hbox{Perfectly secret} $$

$\Rightarrow$) If we have one half as probability of success in the experiment, then this means that the ciphertext is indipendent from the message, stated with maths

$$ \hbox{Pr}\left[\hbox{Priv}\right] = \hbox{Pr}\left[M = m_b \,|\, C = c\right] = {1\over2} $$

$\Leftarrow$)

$$ \eqalign{ \hbox{Pr}\left[\hbox{Priv} = 1\right] &= \hbox{Pr}\left[\hbox{Priv} = 1\,|\,b = 0\right]\cdot\hbox{Pr}\left[b = 0\right] + \hbox{Pr}\left[\hbox{Priv} = 1 \,|\, b = 1\right]\cdot\hbox{Pr}\left[b = 1\right] \cr &= {1\over2}\left\{\hbox{Pr}\left[\hbox{A outputs 0}\,|\,b = 0\right] + \hbox{Pr}\left[\hbox{A output 1}\,|\,b = 1\right]\right\} \cr &= {1\over2}\left\{\hbox{Pr}\left[M = m_0\,|\,C = c, b = 0\right] + \hbox{Pr}\left[M = m_1\,|\,C = c, b = 1\right]\right\} \cr &= {1\over2}\left\{\hbox{Pr}\left[M = m_0\,|\,C = c, b = 0\right] + \hbox{Pr}\left[M = m_1\,|\,C = c, b = 1\right]\right\} \cr &= {1\over2}\left\{\hbox{Pr}\left[M = m_0\right] + \hbox{Pr}\left[M = m_1\right]\right\} \cr &= {1\over2} } $$

2.6: For each of the following encryption schemes, state wheter the scheme is perfectly secret. Justify your answer in each case.

(a) The message space is $M = \left\{0,\dots, 4\right\}$. Algorithm $\hbox{Gen}$ chooses a uniform key from the key space $\{0,\dots, 5\}$. $\hbox{Enc}_k(m)$ returns $\left[k + m \mod 5 \right]$, and $\hbox{Dec}_k(c)$ returns $\left[c - k \mod 5\right]$.
(b) The message space is $M=\{m\in\{0,1\}^l\,|\,\hbox{the last bit of m is 0}\}$. $\hbox{Gen}$ chooses an uniform key from $\{0,1\}^{l - 1}$. $\hbox{Enc}_k(m)$ returns ciphertext $m\oplus\left(k|0\right)$, and $\hbox{Dec}_k(c)$ returns $c\oplus\left(k|0\right)$.

solution

Let's calculate for the part (a)

$$ \eqalign{ \hbox{Pr}\left[C = C\,|\,M = m\right] &= \hbox{Pr}\left[\hbox{Enc}_k(m) = c\right] \cr &= \hbox{Pr}\left[k + m \mod 5 = c\right] \cr &= \hbox{Pr}\left[k = c - m \mod 5\right] \cr &= \begin{cases} {1\over 6} & k\in{1,2,3,4}\,\hbox{i.e}\, m\not= c \ {2\over 6} & k\in{0, 5}\,\hbox{i.e}\, m=c \end{cases} } $$

but this is not independent from from the choose of $m$ so is not perfectly secret.

Instead for the case (b) we have a strange implementation of the one time pad where the messages and ciphertexts have always the last bit set to zero but since that last bit doesn't carry information we can say that is perfectly secret.

2.7

When using the one-time pad with key $k = 0^l$, we have $\hbox{Enc}_k(m) = k\otimes m = m$ and the message is sent in the clear! It has therefore been suggested to modify the one-time pad by only encrypting with $k\not= 0^l$ (i.e. to have $\hbox{Gen}$ choose $k$ uniformly from the set of nonzero keys of length $l$). Is this modified scheme still perfectly secret? Explain.

solution

From theorem 2.10 follows that from an encryption scheme with $|K| < |M|$ you cannot achieve perfect secrecy and in the case where we omit the zero key we are obtaining such case.

2.8

Let $\Pi$ denote the Vigenère cipher where the message space consists of all 3-character strings (over the English alphabet), and the key is generated by first choosing the period $t$ uniformly from ${1, 2, 3}$ and then letting the key be a uniform string of length $t$.

(a) Define $A$ as follow: $A$ outputs $m_0 = aab$ and $m_1=abb$. When given a ciphertext $c$, it outputs $0$ if the first character of $c$ is the same as the second character of $c$, and outputs $1$ otherwise. Compute $\hbox{Pr}\left[\hbox{PrivK}^\hbox{eav}_{A, \Pi} = 1\right]$.
(b) Construct and analyze an adversary $A^\prime$ for which $\hbox{Pr}\left[\hbox{PrivK}^\hbox{eav}_{A, \Pi} = 1\right]$ is greater than your answer from part (a).

Solution

Let's start with the part (a): here we have an adversary that tries to understand which message is sent using "well constructed" ones; for sure, when the key has length 1 it's possible to recognize one message from the other since the same character is encrypted in the same way. Unfortunately for the other cases is not so easy.

However, let's try to calculate the probability of $A$ succeeding:

$$ \eqalign{ \hbox{Pr}\left[\hbox{PrivK}^\hbox{eav}_{A, \Pi} = 1\right] &= \hbox{Pr}\left[A\, \hbox{outputs} \, 0 \,|\, b=0 \right]\hbox{Pr}\left[b=0\right] + \hbox{Pr}\left[A \,\hbox{outputs} \, 1 \,|\, b=1 \right]\hbox{Pr}\left[b=1\right] \cr &= {1\over2}\hbox{Pr}\left[\hbox{Enc}(aab) = xxy\right] + {1\over2}\hbox{Pr}\left[\hbox{Enc}(abb) = xyz\right] \cr &= {1\over6}\sum_{ \hbox{key lengths} }\bigl(\hbox{Pr}\left[\hbox{Enc}_k(aab) = xxy\right] + \hbox{Pr}\left[\hbox{Enc}_k(abb) = xyz\right]\bigr) \cr &= {1\over6}\bigl(\hbox{Pr}\left[k=\alpha\right] + \hbox{Pr}\left[k=\alpha\alpha\right] + \hbox{Pr}\left[k=\alpha\alpha\beta\right] \cr &\phantom{=} + \hbox{Pr}\left[k=\alpha\right] + \hbox{Pr}\left[k=\alpha\alpha\right] + \hbox{Pr}\left[k=\alpha\alpha\beta\right]\bigr) \cr &= {1\over6}\bigl(1 + {1\over N} + {1\over N} + 1 + {N - 1\over N} + {N - 1\over N}\bigr) \cr &= {2\over 3} \cr } $$

$$ {1\over6}\sum_{\hbox{key lengths}}\bigl(\hbox{Pr}\left[\hbox{Enc}_k(aab) = xxy\right] + \hbox{Pr}\left[\hbox{Enc}_k(abb) = xyz\right]\bigr) $$

Note that the case $\hbox{Pr}\left[\hbox{Enc}(abb) = xyz\right]$ for situation with key length greater than one is very likely: indeed once selected the first character ($N$ choices), all the remaining but one give a different resulting second character in the ciphertext so we have ${N - 1\over N}$ possibilities. This value is just right to remove the unlikely to obtain from a plaintext with two initial equel characters a ciphertext with the first two initial characters that remain equal: this means that if remove the possibility to encrypt with key of length one we have a perfectly secret cipher.

This explain the result: guessing completely random, we have ${1\over 2}$ probability of guessing for each key length that has a probability of appearing like ${1\over3}$; but in our case we are able to always distinguish when the key has length one, so we have ${3\over6} + {1\over6}$.

This can help us for part (b): if we are able to distinguish always messages with key length equal to two we can add another ${1\over6}$ to our chances!

$A^\prime$ outputs $m_0=aaa$ and $m_1=abb$. When given ciphertext $c$, it outputs $0$ if the first character of $c$ is the same as the second character and third character of $c$, and outputs $1$ otherwise.

TODO

2.9

in this exercise, we look at different conditions under which the shift, mono-alphabetic substitution, and Vigenère ciphers are perfectly secret:

(a) Prove that if only a single character is encrypted, then the shift cipher is perfectly secret.
(b) What is the largest message space $M$ for which the mono-alphabetic substitution cipher provides perfect secrecy?
(c) Prove that the Vigenère cipher using (fixed) period $t$ is perfectly secret when used to encrypt messages of length $t$.

Reconcile this with the attacks shown in the previous chapter.

Solution

For (a) we can use the Shannon's theorem: for the shift cipher, in the case with only one character, we have $| M | = | K| = | C |$ hence it's perfectly secret iff $\forall m\in M, \forall c\in C, \exists! k\in K $ such that $\hbox{Enc}_k(m) = c$; this is indeed the case.

For (b) instead we can start considering the fact that the mono-alphabetic substitution cipher has the key space fixed (with size $26!$); another trivial consideration is that for messages of length one this cipher is equivalent to the shift cipher of the case (a), so it's perfectly secure. An upper limit is given by the consideration that when $|M| \gt|K|$ we cannot have a perfectly secret cipher, this makes realize that since $26^2\gt26!$, the maximum size for the message space of the mono-alphabetic substitution cipher is one;

For the situation described in (c), using again the Shannon's theorem we have that it's a perfect cipher.

TODO: part about the previous chapter.

def f(steps):
    N = 26
    result = 1
    while N > steps:
        result *= N
        N -= 1
    return result


>>> [(26**_, f(26 - _)) for _ in range(1, 27)]

[(26, 26),
 (676, 650),
 (17576, 15600),
 (456976, 358800),
 (11881376, 7893600),
 (308915776, 165765600),
 (8031810176, 3315312000),
 (208827064576, 62990928000),
 (5429503678976, 1133836704000),
 (141167095653376, 19275223968000),
 (3670344486987776, 308403583488000),
 (95428956661682176, 4626053752320000),
 (2481152873203736576, 64764752532480000),
 (64509974703297150976, 841941782922240000),
 (1677259342285725925376, 10103301395066880000),
 (43608742899428874059776, 111136315345735680000),
 (1133827315385150725554176, 1111363153457356800000),
 (29479510200013918864408576, 10002268381116211200000),
 (766467265200361890474622976, 80018147048929689600000),
 (19928148895209409152340197376, 560127029342507827200000),
 (518131871275444637960845131776, 3360762176055046963200000),
 (13471428653161560586981973426176, 16803810880275234816000000),
 (350257144982200575261531309080576, 67215243521100939264000000),
 (9106685769537214956799814036094976, 201645730563302817792000000),
 (236773830007967588876795164938469376, 403291461126605635584000000),
 (6156119580207157310796674288400203776, 403291461126605635584000000)]

Notes

Exercises

solution

solution

solution

solution

solution

solution

2.7

solution

2.8

Solution

2.9

Solution

Comments